stars

Stars are integral to worldbuilding especially if you are constructing an entire solar system.

classes

class	temperature (K)
O	33000+
B	10500–30000
A	7500–10000
F	6000–7200
G	5500–6000
K	4000–5250
M	2600–3850

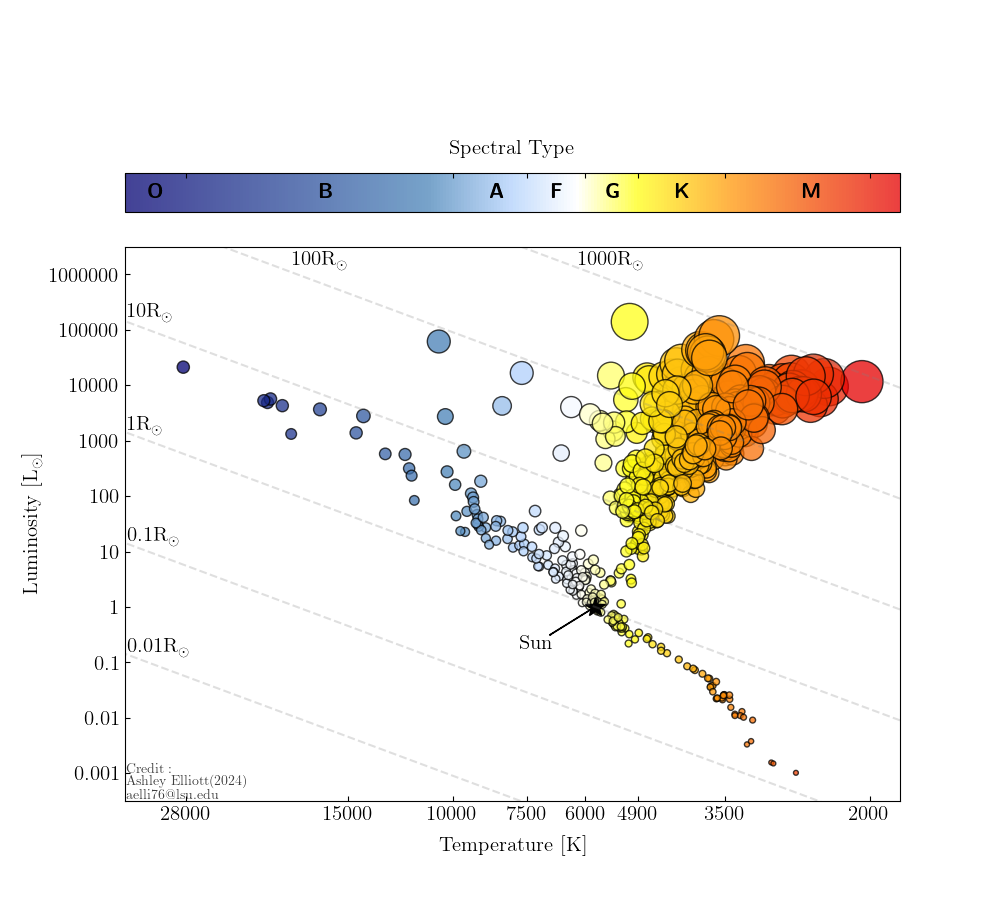
HR diagram by Ashley Elliot (Louisiana State University) — Hertzsprung–Russell diagram by Ashley Elliott, LSU. Source

The Hertzsprung–Russell diagram shows the relationship between stars’ spectral types, radii, luminosities, and effective temperatures.

The Sun is a G-type main-sequence star. Main sequence refers to the diagonal line that runs roughly from the upper left to the lower right of the diagram above.

mass

Mass is a key value here as almost every other attribute of the star can be derived from it. Stellar mass is expressed in solar masses (M_☉). A 2 M_☉ star has twice as much mass as our Sun. Stars can be as small as 0.09 M_☉ to as big as 150 M_☉.

1 M_☉ = (1.98847 ± 0.00007) · 10³⁰ kg

temperature

The following equation gives an approximate temperature (T ) of a star given its B-V color index:

T = 4600 * (1 / (0.92BV)  + 0.62) + (1 / (0.92BV) + 1.7)

luminosity

Luminosity is the amount of energy emitted by an astronomical object—a star in this case. A star’s luminosity is expressed in terms of solar luminosity (L_☉), which is ~3.828 × 10²⁶ watts, and derived from its size and effective temperature. Read more about mass–luminosity relation.

// mass–luminosity relation
L_☉ = M_☉^a

For main-sequence stars, a is set to 3.5. Things get tricky because of the Eddington luminosity, which sets a limit to a star’s normal luminosity. If exceeded, the star loses mass. The table below gives the approximate formulæ based on mass range where M is your chosen star’s mass.

mass	luminosity
`M` < 0.43 M_☉	`L_☉ ≈ 0.23 × M_☉^2.3`
0.43 M_☉ < `M` < 2 M_☉	`L_☉ = M_☉⁴`
2 M_☉ < `M` < 55 M_☉	`L_☉ ≈ 1.4 × M_☉^3.5`
`M` > 55 M_☉	`L_☉ ≈ 32000M_☉`

Alternatively, luminosity can also be derived from a star’s radius and effective temperature.

L_☉ = 4πR_☉²σT⁴

σ is the Stefan–Boltzmann constant which is ~5.67 × 10^-8 W/(m²K⁴).

radius

Radius (R_☉) can be calculated using luminosity. 1 R_☉ = 695700 km.

R_☉ = sqrt(L_☉/4πσT⁴)

An alternate way of calculating diameter (and radius) based on temperature and luminosity:

d ≈ (5770² / T²) * sqrt(L_☉)
R_☉ = d / 2

surface area

A = 4πr²
A = πd²

lifetime

A star’s lifetime (τ) can be estimated using its mass. 1 τ = 10 × 10⁹ years (10 billion).

τ ≈ 10¹⁰ * M_☉^2.5

resources

Stellar Lifetimes — Georgia State University